例題1 確率変数 X が標準正規分布 N(0,1 2) に従うとき,次の確率を求めよ。 (1) P(067≦X≦164) (2) P(121≦X≦0) 解答右のシュミレーションを用いて,求めることにしましょう。数表に載っているI(a)に直すのに, グラフで幾何的に考えて説明していますが,I(z)=I(z), I(∞)=1/2, I(0)=0, I(∞)=1/2 から機械的に単純化することも確率値 p 正規分布表を用いた確率計算の例題 :製品の品質管理 • テキスト61ページの例題5.1:「品質管理」 化粧品のボトル。工場でのボトル詰め工程により、実際 にボトル詰めされた製品の容量にはバラツキが生じて しまう。

確率統計 正規分布 の問題です 大学の確率統計の問題なんですがさっ 数学 教えて Goo
正規分布 確率 例題
正規分布 確率 例題-標準正規分布で上側確率02 となるときの面積を調べます(答えは0842)。そこから 60 0842 10 X という 式を立てて、これを解くとX 60 0842u10, X 684となり、上から1 万人目の学生の得点は68 点から 69 点と推定することができます。Quiz(2次元正規分布) 次の2変数確率密度関数は2次元正規分布を定める f(x;y) = C e 24x 1 6y 22y 1 X;Y の母平均値, 母分散, 母共分散を求めよう 2 E1 = 1 が満たされるように定数C を定めよう 樋口さぶろお(数理情報学科) L11 2 次元正規分布 確率統計☆演習II(16) 12 / 22




2次元正規分布の確率密度関数から母平均値 母分散行列 Youtube
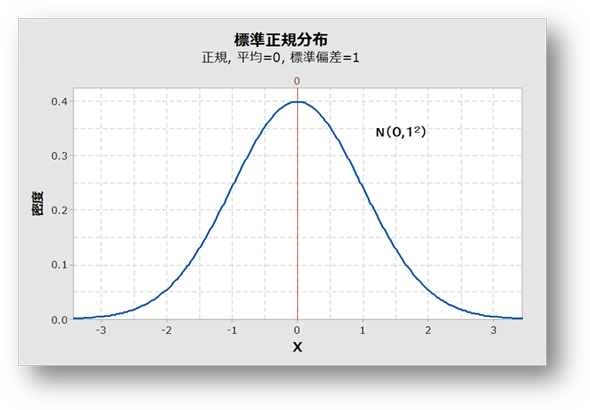
標準正規分布 正規分布 の基本形ともいえる 標準正規分布 について議論する 一般に, ある正規分布に従う確率変数がある範囲内に得られる確率は, 標準正規分布を用いて計算することが出来る したがって, 標準正規分布に従う確率変数の値がある範囲内に平均の異なる正規分布 x f(x)10 0 10 30 000 005 010 015 0 分散の異なる正規分布 x f(x) N 5,4 N 10,4 N 10,4 N 10,25 x = のとき確率密度関数f (x) の ⾼さが最⼤になる。 正規分布の平均 が10 から5 に 変わるとき,分布の「⼭」⾃体 が平⾏移動する。例3 標準正規分布の確率 標準正規分布の確率 下に示した確率は,統計パッケージ及び 参考書等の付表より得られる 0 196 0 196 0475 0475
表1の標準正規分布で確率変数Kp=252 の確率をもとめると、P= つまり、3094% の確率で1556 より大きい値が得られるという結果になります。 \\ ⑤正規分布表の見方 PかX ¯ の確率分布図を考える 最初に、標本平均 X ¯ の確率分布曲線のグラフを描く。 この問題では母集団がどんな分布か分からない。 でも、 100 は十分に大きい数と考えるので、上の復習より、 X ¯ は近似的に正規分布 N ( μ, 255 2 100) に従う。 この確率3 正規分布(normal distribution)の定義 (1) 連続的確率変数 の密度関数 が (ただし, P,V は定数で, ) であるとき, は正規分布 N(P,V2) に従うといい, ~ N(P,V2) で表す。(式の中の は円周率 である。) (2) 次が成立する。 定理(正規分布の平均・分散) X ~ N
正規マルコフ情報源の定常分布 10 情報理論講義資料#5 十分時間が経過すれば,初期分布がどうであれ,状態分布は 定常的な確率分布(定常分布)に落ち着く. 正規マルコフ情報源が落ち着く定常分布を 𝒘=( 0, 1,・・・, −1)確率システム 5 手順 • 累積確率F(x)、確率変数xに対して式を変形 しG(F)=aH(x)bとなるよう誘導する • 縦軸にG(F)目盛りを、横軸にH(x)目盛りを付 けたものが、この分布形状に対する確率紙と なる • この分布形に適合する場合(xi,Fi)をプロットし熊本大学数理科学総合教育センター (7) x は正規分布n(10,152) に従い, y は正規分布n(10,) に従うものとするこの とき確率p(10 < x y < 30) を求めよ 解 正規分布の再生性より, 確率変数x y は正規分布n(,2) に従うした がって変数変換した確率変数
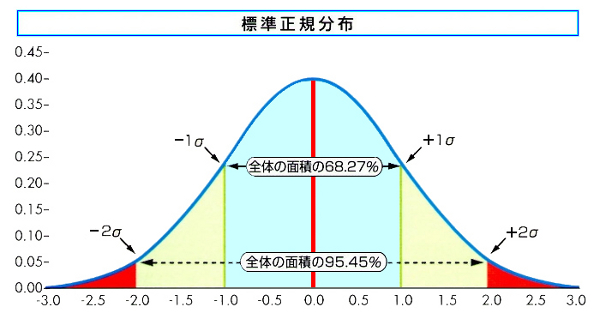



分かりやすい統計学 標準正規分布による確率計算と分布表の見方 ミナピピンの研究室




確率分布の使い方 正規分布 データ分析教室 Nava ナバ
対数正規分布の期待値は,以下の2通りの方法で計算できます。 方法1 対数正規分布の期待値を定義から直接計算する つまり, E X = ∫ 0 ∞ x f (x) d x EX=\displaystyle\int_0^{\infty} xf(x)dx E X = ∫ 0 ∞ x f (x) d x 方法2 Y Y Y が正規分布に従うとき, e Y e^Y e Y の期待定理71 2つの確率変数X;Y に対して, その積率母関数が一致するならば, すなわち, MX(t) = MY (t)が成り立つならば, X とY が従う確率分布は同じである 代表的な確率分布の積率母関数を具体的に求めてみよう 例題71 X が2項分布B(n;p)に従うとき, 次が成り立つ MX(t回数の多い反復試行の確率は、正規分布表を使って求める。 この方法は完全にパターン化していて、やり方さえ知っていれば機械的に計算できるので、方法を憶えておいてほしい。 以下、 1 二項分布を正規分布で近似する 2 正規分布を標準化する 3




標準分布第五章 Voajcr




正規分布の期待値の求め方 理数アラカルト
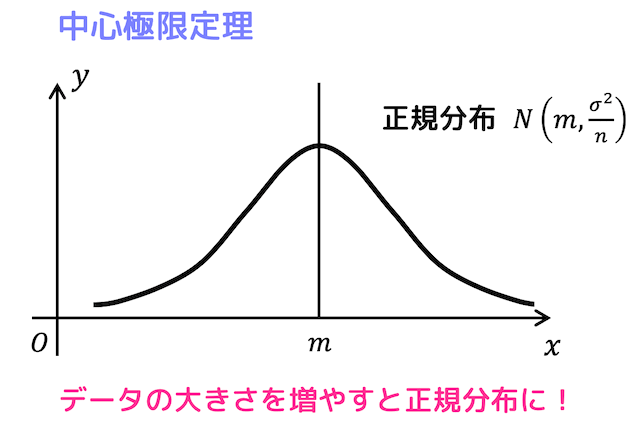
正規分布の利用例 1 正規分布の利用例 面積 (確率)の求め方 ジュースやお菓子の袋の重さ,ボルトやナットの長さ,また,身長や体重,月ごとの漁獲高など,大量のものから1つを選ぶとき,その変量の値 X の確率密度関数は, となります (詳しい説明は第8回:正規分布(2回目) 正規分布表を用いた確率計算の例題 :製品の品質管理 • テキスト61ページの例題5.1:「品質管理」 化粧品のボトル。工場でのボトル詰め工程により、実際 にボトル詰めされた製品の容量にはバラツキが生じて しまう。この例題では母集団が正規分布 に従うことを仮定している.したがっ て,標本平均 は正規分布 に従う 命題 .つまり,確率密度 関数 に従う 式 .このとき,標本平均 が の値をとる確率は, である 式 . 母平均 に対して,次式を満たす定数 があったと




正規分布



確率統計標準正規分布次の画像の例題をやっているのですが この解き方だとx Yahoo 知恵袋
正規分布とは 正規分布とは、データが平均値付近に集まって、平均値を境に左右対称にばらついた分布です。 正規分布は、統計学において最も重要な確率分布の1つです。 なぜなら、多くの統計的手法は「データが正規分布に従うこと」が前提として考え 1-4.Juliaで例題を解いてみる Juliaで分布を扱うための基礎知識は以下のページを参照してください。 「Juliaで学ぶ確率変数(1) 確率変数の定義」の「4.Juliaで確率分布を扱う」 Juliaでは正規分布の確率密度の定義はDistributionsNormalを使います。2 確率変数x が正規分布n(5,22) に従うとき, 確率p(x ≥ 7) を求めよ 解 確率変数をz = x − 5 2 とおくと, z は標準正規分布n(0,1) に従う このとき求め る確率は, 標準正規分布表を使うと, p(x ≥ 7) = p(z ≥ 1) = 05 − p(0 ≤ z ≤ 1) = 05 − =




確率分布からの乱数の生成1 確率変数の変換 Daily Tech Blog



正規分布とは 表の見方や計算問題をわかりやすく解説 受験辞典
正規分布確率密度関数 Author 張 南 Last modified by NaN Zhang Created Date 10/6/00 14 AM 分布の諸変数 標準正規分布の性質(p116) 性質の説明 証明: 証明: 練習問題 二項分布の正規分布による近似 例題 , 練習問題:p125, 問題5 正規分布を標準正規分布に変形することを、標準化といいます。 (正規分布について詳しく知りたい方は正規分布とは?をご覧ください。) 正規分布を標準化する式 確率変数\(X\)が正規分布\(N(μ,σ^2)\)に従うとき、 $$ Z = \frac{Xμ}{σ} $$ と変換すると、\(Z\)は標準正規分布\(N(0標準正規分布N(0,1) に従う確率変数Z について,実数a, b ( a ≤ b ) に対して, これらの公式と正規分布表とを用いて,標準正規分布N(0,1) に関する確率を計算 します. 例題 351 標準正規分布N(0,1) に従う確率変数Z について,確率P( Z ≤123 ) ,



Http Www3 U Toyama Ac Jp Kkarato 16 Statistics Handout Statistics 16 11 0524 Pdf



14 6 標準正規分布の使い方2 統計学の時間 統計web
標準正規分布表の使い方についての問題です。145章で示した標準正規分布表(上側確率についての標準正規分布表)には がとる値が 以上となる確率 が示されています。この表から =0となる数値を探すと、「0023」という値が得られます。したがってしたがってx は近似的に正規分布n(0,102) に従う pb を二項分布b(400,05) にお ける確率, pn を正規分布n(0,102) における確率とすると, 求める確率は pb(180 ≤ x ≤ 2) ≑ pn(180 ≤ x ≤ 2) となり, 正規分布の確率で近似計算が行える 1正規分布とは 正規分布(ガウス分布)とは,図のような左右対称の連続型の確率分布です。 正確な定義(確率密度関数)については後述します。 正規分布は最も代表的な分布の一つです。 例えば物理などの実験における測定の誤差,テストの点数など



統計検定対応 正規分布から確率を求める問題の解き方 統計学 確率 オザワの統計学ブログ



エクセルでの正規分布の計算
二項分布B(30, 1/6)と正規分布N(5, 25/6) 0 005 01 015 02 025 x 確率(密度)分布 B(30, 1/6) N(5, 25/6) 正規分布の応用あれこれ(続き) ②微分方程式(拡散方程式)の解としての 正規分布 時間とともに分散が大きくなっていくような 正規分布N(0, 2Dt) に従う例題︓正規分布のグラフの⾒⽅ 17 「μ-σ 以上μ 以下になる確率」 = 『オレンジで塗りつぶされた部分の⾯積』 ↓ 正規分布グラフのある範囲の⾯積は、 その確率を表す。 Waku2バーガーのポテトの⻑さ 平均値μ=457cm 標準偏差σ=0cm 正規分布に従うと中心極限定理と正規近似 指数分布と正規分布と応用 正規分布の例題 L11Q2 Quiz(正規分布の応用) ある試験を受験したときの点数は連続型確率変数X で, 母平均値50, 母 分散102 の正規分布にしたがうという 点数が60から65である確率を求 めよう
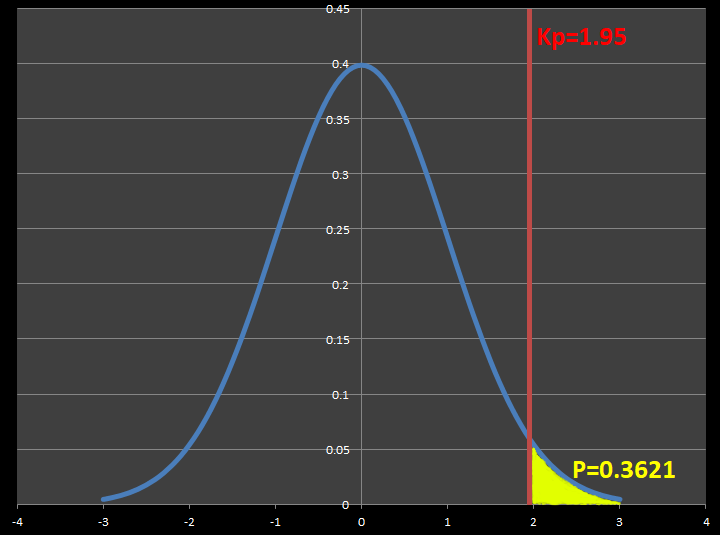



Qc検定2級 統計 正規分布表 見方 意味 ニャン太とラーン




中心極限定理の例とメリットをわかりやすく解説 Avilen Ai Trend
連続型確率変数 正規分布(normal distribution) 確率変数X が–∞ から∞ までの間の実数を取り、その 密度関数が で与えられている時、確率変数X は正規分布に従って いるという。ここでexp a はea を、e は自然対数の底 (e = )を表している。, 2 ( ) exp 2 1連続型確率変数 答のひとつは f(x) = 1 4 p 3 ( 2 p 3 x < 2 p 3) 0 (他)解答例2 既存のX に対して, EaX b = aEXb, VaX b = a2VX を使っ て, Y = aX b が希望の値になるように調整する 確率密度関数f(x) は平行移動, 拡大縮小される 樋口さぶろお(数理情報学科) L08 正規分布・確率変数の変数変換 確率確率分布の基本を分かりやすく解説片手間ブログ QC検定3級における正規分布の「たった一つの攻略法」とは? 確率分布の基本を分かりやすく解説 皆さんはデータのばらつきを視認するとしたらどのような方法で試みますか? ばらつきをより分かり




正規分布の利用例




確率分布の使い方 正規分布 データ分析教室 Nava ナバ
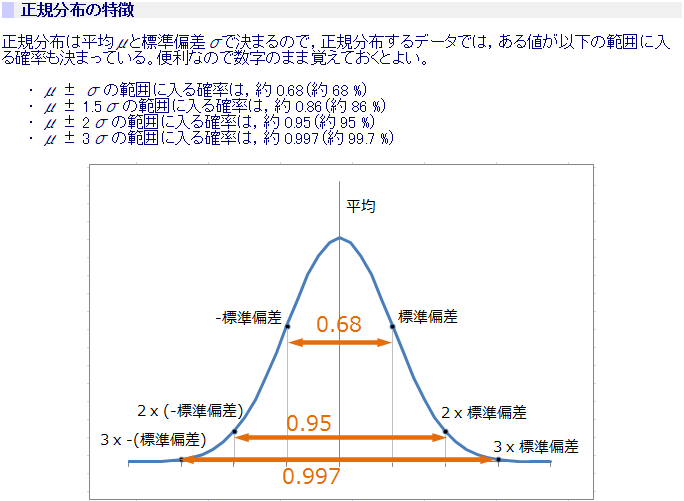
正規分布では(平均)±196×(標準偏差)の範囲に入る確率は95%になる.( z=196 のときの正規分布表の値が 0475 だから両側で 095 になる.) ※ 標本平均 の標準偏差として利用するもの正規分布の例 同質性の高い集団における各人の身長はおおよそ正規分布に従うと言われています。 仮に、日本人成人男性をランダムに一人抽出した時のその人の身長を確率変数Xとすると、Xが平均μ=171cm、分散σ 2 =64の正規分布に従うとします。 (これは筆者の肌感覚で大体正しいと思われる確率論や統計学で用いられる正規分布(せいきぶんぷ、英語 normal distribution)またはガウス分布(Gaussian distribution)とは、平均値の付近に集積するようなデータの分布を表した連続的な変数に関する確率分布である。




確率がわかる ファーストブック Amazon Com Books




確率統計 正規分布 の問題です 大学の確率統計の問題なんですがさっ 数学 教えて Goo
正規分布に従う確率変数 X〜N(μ,σ2)がc≦X<dとなる確率を, 標準正規分布Z〜N(0,1)の上側確率Q(u)の表から求めるQ(u)=P(Z ≧ u)=∫_u^∞ f(z)dz高校の数学Bの教科書などにはI(u)=∫_0^u f(z)dz= 1/2Q(u)の表が載ってることもあります



標準正規分布表を用いて次の確率を求める問題が分からないので助け Yahoo 知恵袋



確率分布のベイズ推定 正規分布に従う場合




二項分布と正規分布



標準正規分布 Taustation




標準正規分布による推定 小西研究室 電脳工房msc Atwiki アットウィキ




統計検定準1級 2次元正規分布と条件付き確率分布の求め方 R Goodな生活




E資格 例題 正規分布 ポアソン分布 Klダイバージェンス フグサカ Note
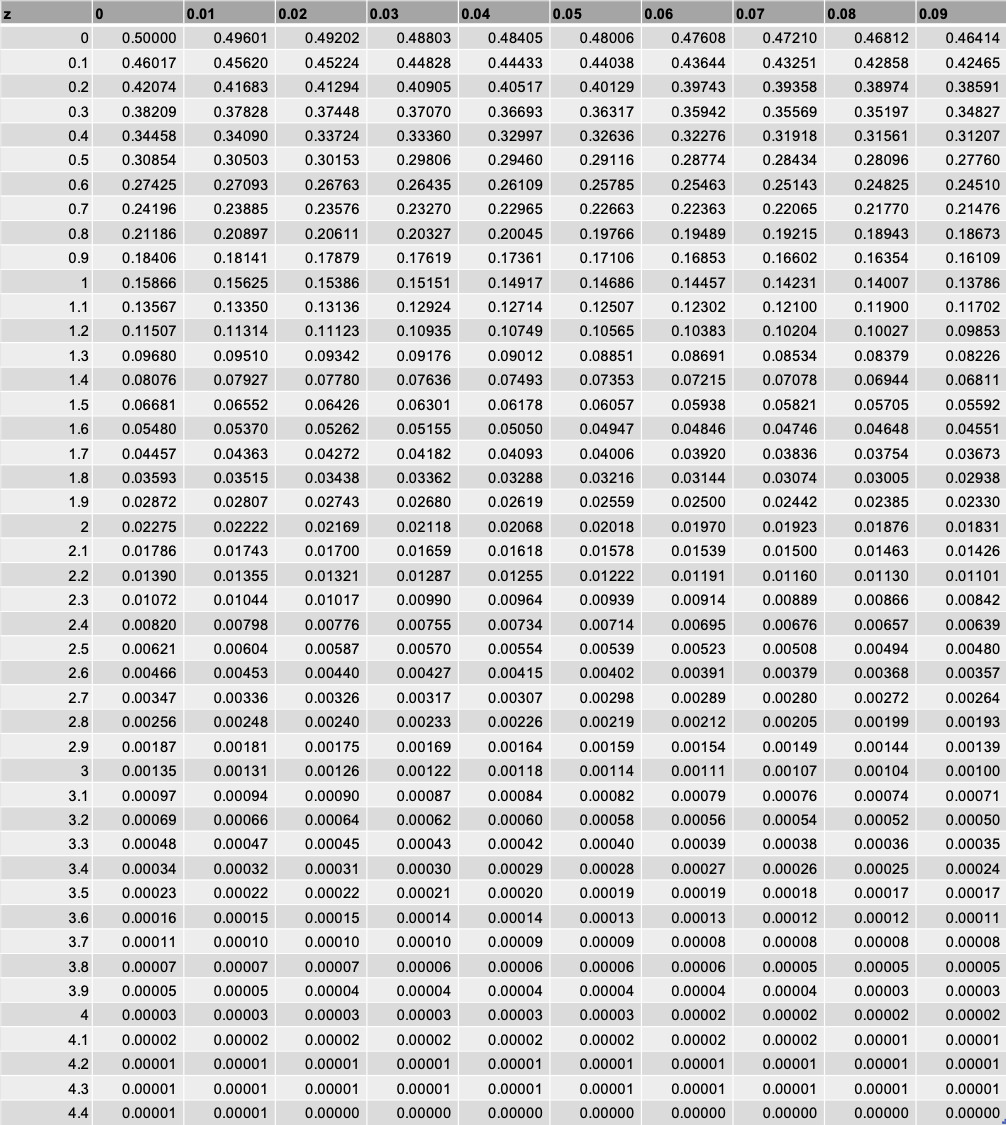



標準正規分布表の見方や使い方 標準化やz値の計算式はどうすればいい いちばんやさしい 医療統計
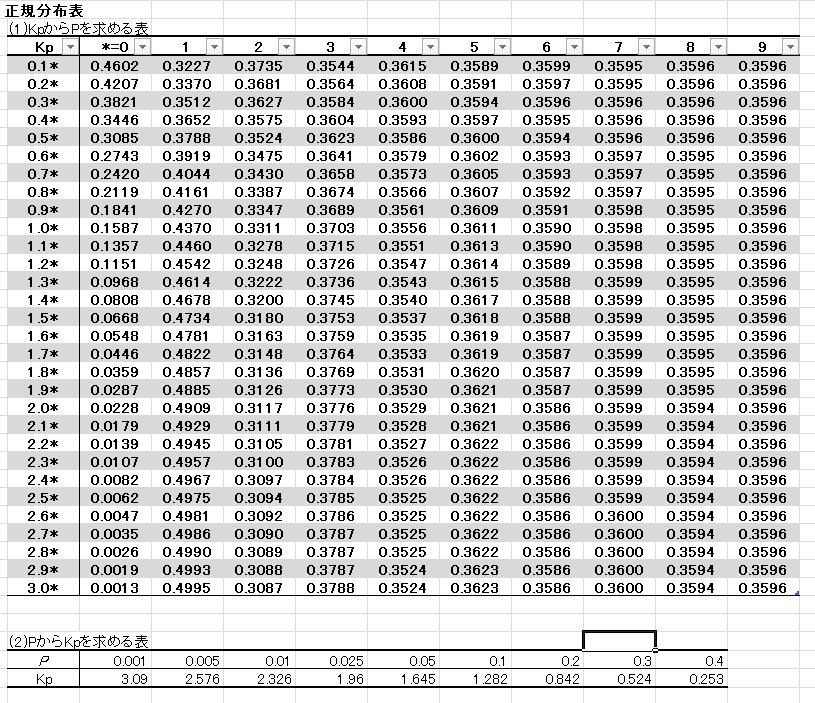



Qc検定2級 統計 正規分布表 見方 意味 ニャン太とラーン
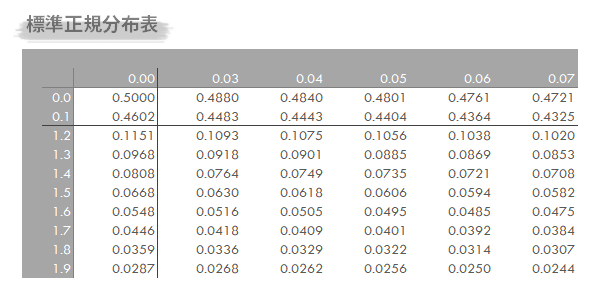



標準正規分布の確率とパーセント点の計算 With Excel




正規分布確率密度関数 Ppt Download




チョコっと正規分布




第8回 二項分布の近似 ポアソン分布 正規分布 Ppt Download




高校数学 確率分布と統計的な推測 きのむくままに
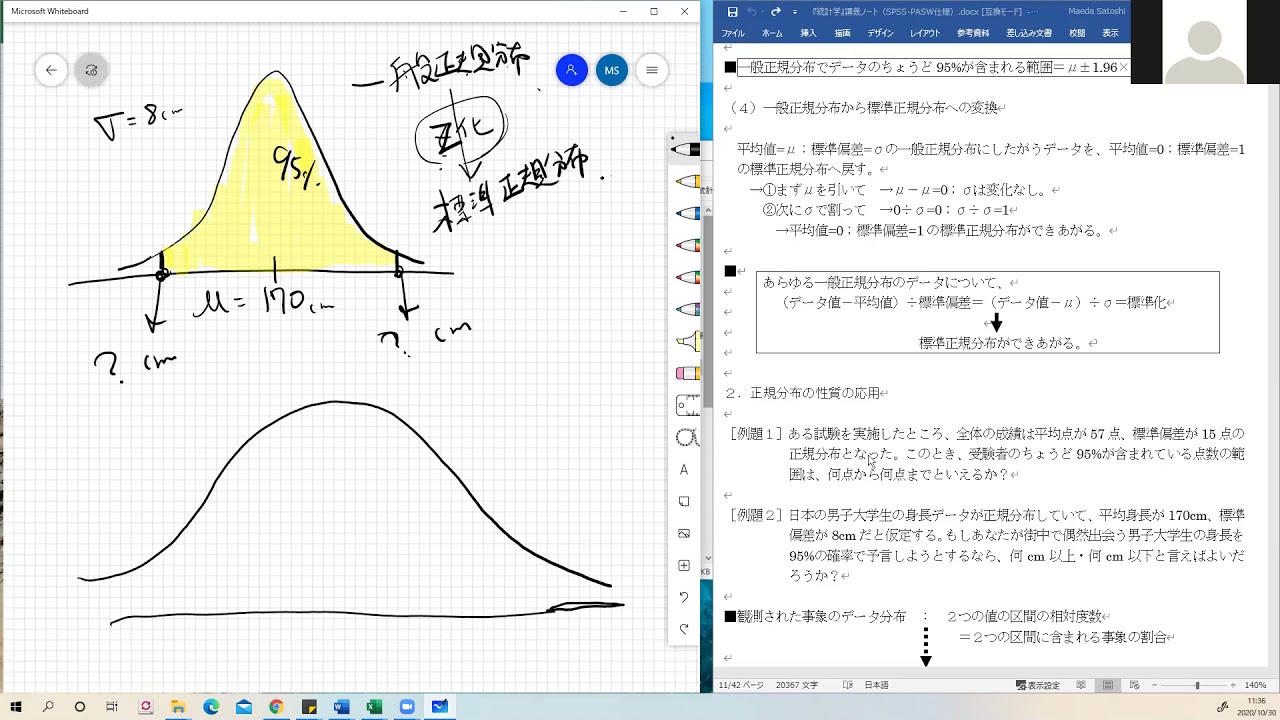



文系のための統計学入門 4 2 標準正規分布の性質を使って95 の確率で予測する Youtube
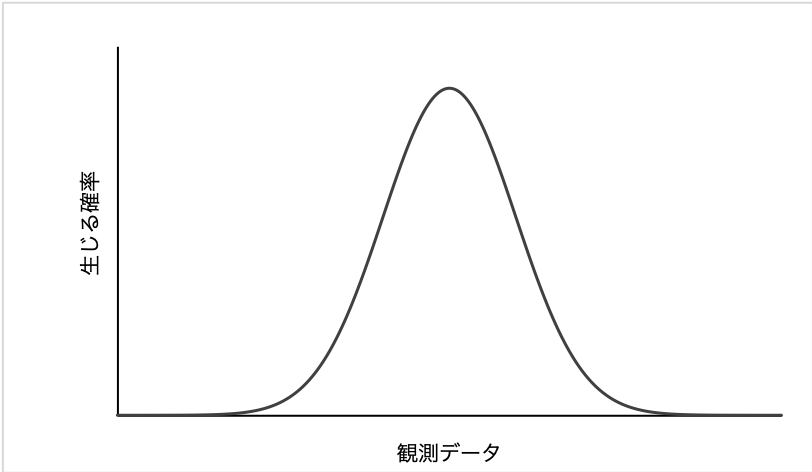



確率密度関数とは わかりやすく正規分布一様分布の面積が確率になる意味を いちばんやさしい 医療統計



統計學 馬場敬之スバラシク実力がつくと評判の統計学キャンパス ゼミ改訂3 蝦皮購物
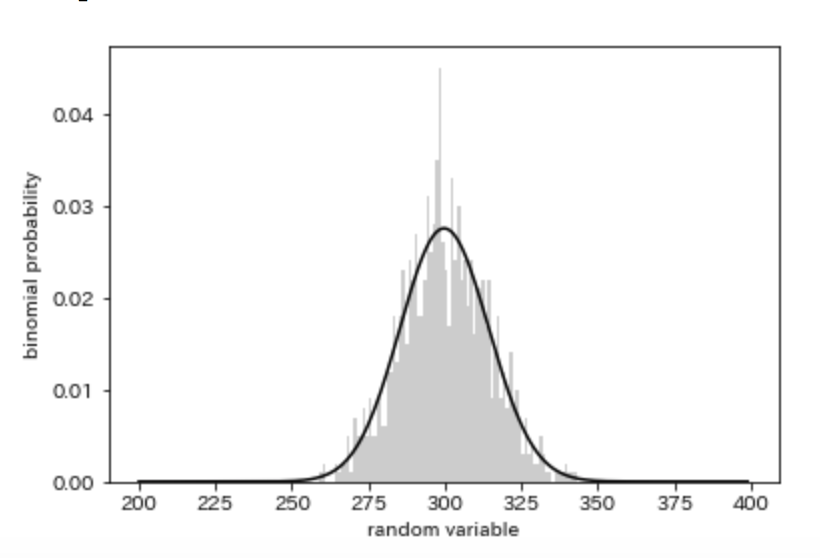



Pythonで学ぶ二項分布と正規分布の関係性 Case Kの備忘録



正規分布とは 表の見方や計算問題をわかりやすく解説 受験辞典




正規分布を用いた練習問題 小西研究室 電脳工房msc Atwiki アットウィキ




標準偏差って何 例題でわかりやすく順を追って解説 正規分布も噛み砕いてみました 機械設計者の皆様 教わらなかったことは常識だそうです



統計検定対応 正規分布から確率を求める問題の解き方 統計学 確率 オザワの統計学ブログ




確率分布の使い方 正規分布 データ分析教室 Nava ナバ




正規分布の分かりやすいまとめ Avilen Ai Trend



正規分布とは 表の見方や計算問題をわかりやすく解説 受験辞典



第回 統計数理講座 検定法の導出 正規分布に関する検定 仮説検定 基礎から分かる統計学




確率分布の使い方 正規分布 データ分析教室 Nava ナバ



統計学演習 第5章 正規分布




2次元正規分布の確率密度関数から母平均値 母分散行列 Youtube



Rで多次元正規分布に従う乱数を生成する 年金運用の例題付き



正規分布とは 表の見方や計算問題をわかりやすく解説 受験辞典




コイン投げから分かる二項分布 正規分布やポアソン分布との関係性と近似について アタリマエ




正規分布から工程能力を理解する た とるのミリオネアへの道



14 5 標準正規分布表の使い方1 統計学の時間 統計web




正規分布とは 意味と性質 標準正規分布表の読み方まで徹底解説



正規分布とは 表の見方や計算問題をわかりやすく解説 受験辞典
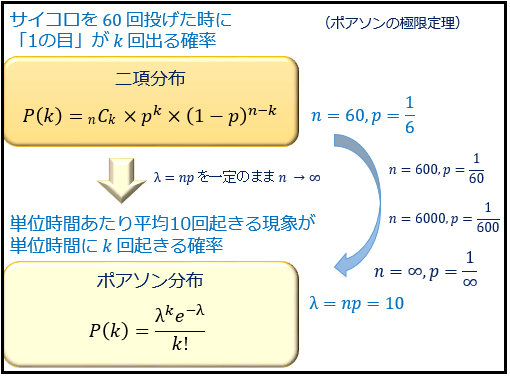



ポアソン分布とは何か その性質と使い方を例題から解説 馬に蹴られて死ぬ兵士の数を予測した数式 アタリマエ



Sec4
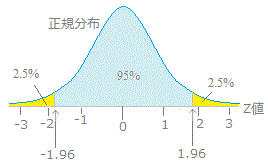



問題練習 母平均の推定 信頼区間
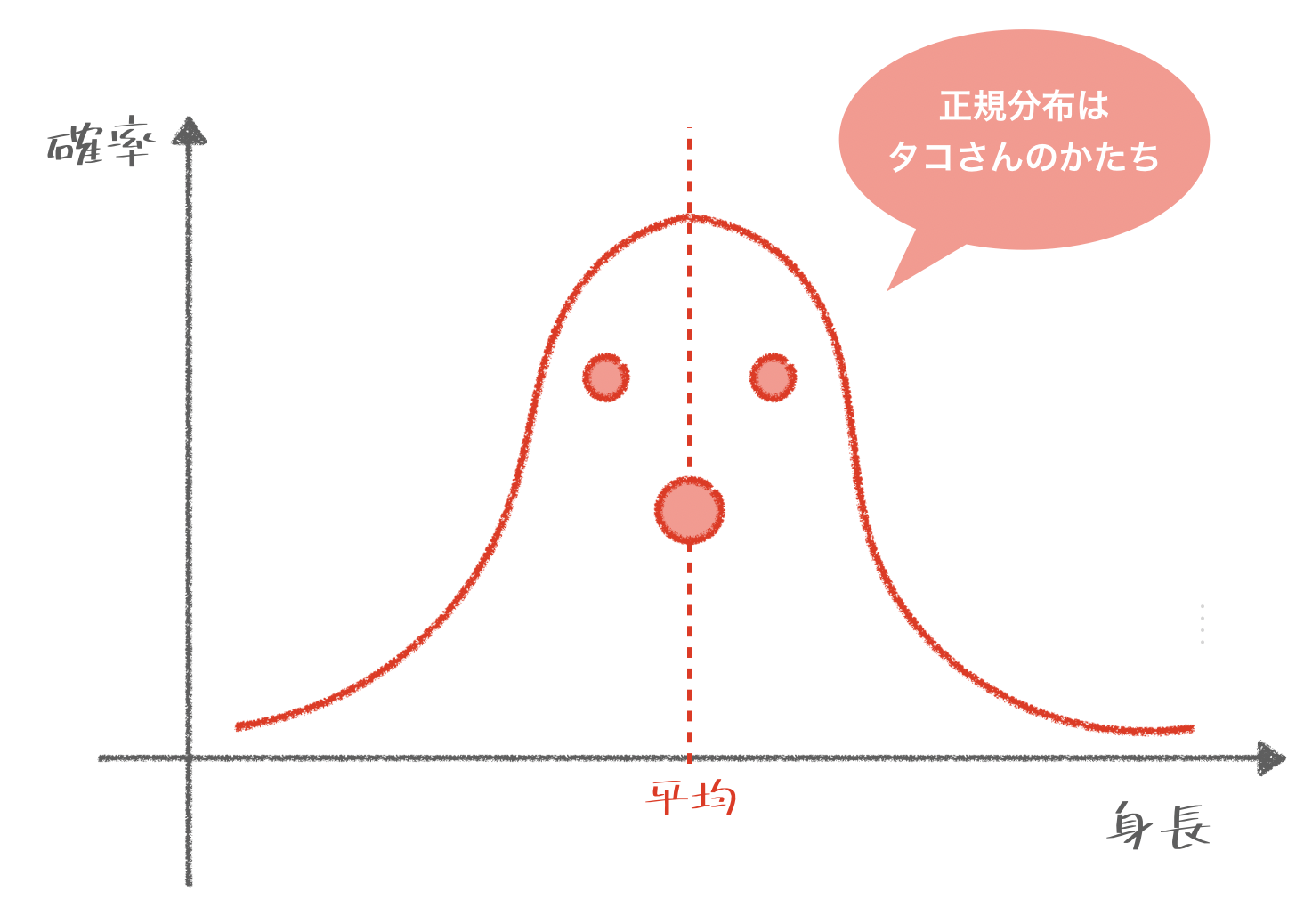



初学者向け 正規分布は タコさん のかたちと覚えよう やさしく図解 ふわっと理解 小学校の知識でわかる統計辞書



3sと不良品発生の確率を予測する 標準正規分布表 3d設計推進者の眼 31 2 4 ページ Monoist



R Source



正規分布と推定 検定 確率 統計 web教材 木暮



正規分布




正規分布とは何なのか その基本的な性質と理解するコツ アタリマエ



Juliaで学ぶ確率変数 5 正規分布 連続型 Qiita



正規分布とは 表の見方や計算問題をわかりやすく解説 受験辞典



以下の問題を解答するにあたっては 必要に応じて次ページの正規分布表を用いて もよい あ



正規分布とは 表の見方や計算問題をわかりやすく解説 受験辞典



Www Oit Ac Jp Is Shinkai Lecture Probstat13a Ps13 05 06 Pdf



第4回 データの表現と把握2 データの分布とばらつき




例題解説 正規分布の確率を標準正規分布表から求める Youtube



正規分布とは何なのか その基本的な性質と理解するコツ アタリマエ




標準分布第五章 Voajcr



1週間で完成 うさぎでもわかる確率分布と統計的な推測 6日目 母平均 母比率の推定 工業大学生ももやまのうさぎ塾




問題14 全部 確率分布ノート 解説動画 チャート式の数研出版




ヒストグラムと密度曲線



二項分布と正規分布 確率分布と統計的な推測 おおぞらラボ



確率 確率分布関数 確率密度関数



統計学演習 第5章 正規分布




例題解説 正規分布n M S2 の確率を対応する標準正規分布n 0 1 の確率に書き直して求める Youtube




X2分布
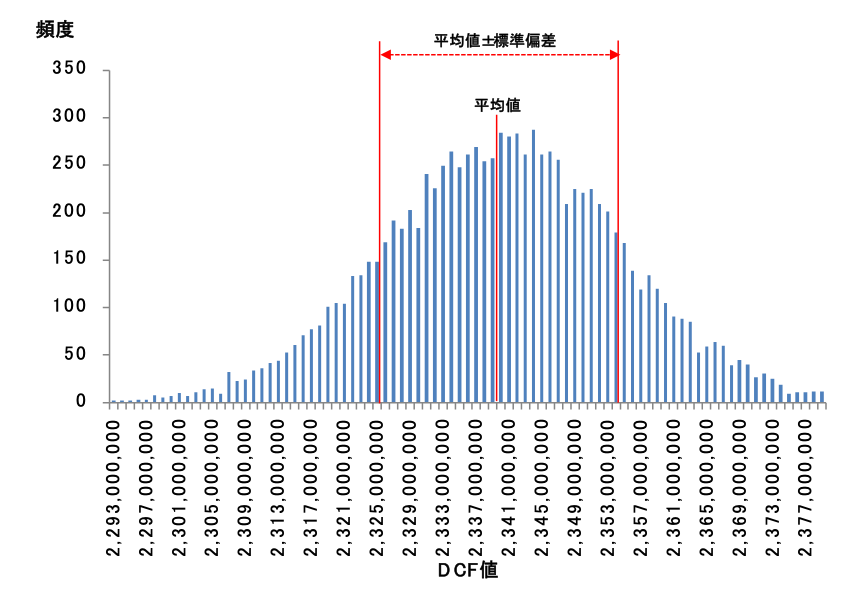



賃貸住宅のddcf法の値の考え方 株式会社タス
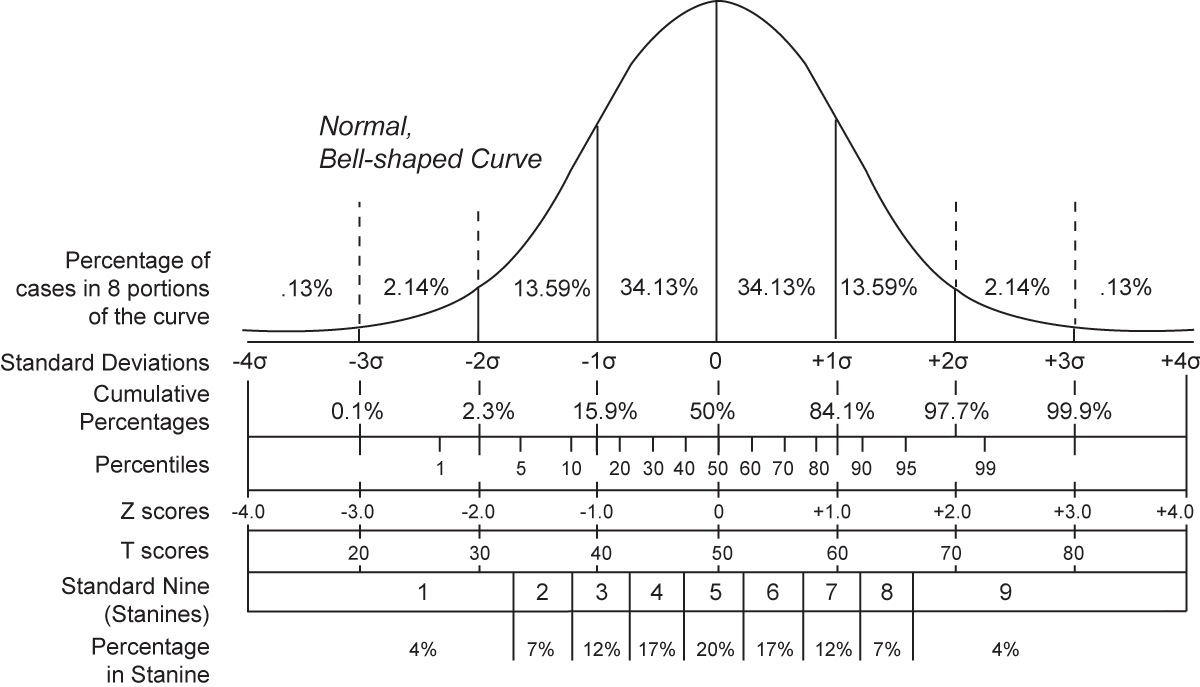



正規分布に従う検定統計量を利用した平均値の検定 Z 検定



確率統計の問題です 第二種の誤りを犯す確率です 例題1 2 の答えがなぜ Yahoo 知恵袋




正規分布を標準化する方法と意味と例題と証明 Avilen Ai Trend



14 5 標準正規分布表の使い方1 統計学の時間 統計web




正規分布から工程能力を理解する た とるのミリオネアへの道



13 3 ポアソン分布 統計学の時間 統計web



正規分布



統計学の基礎 9 26
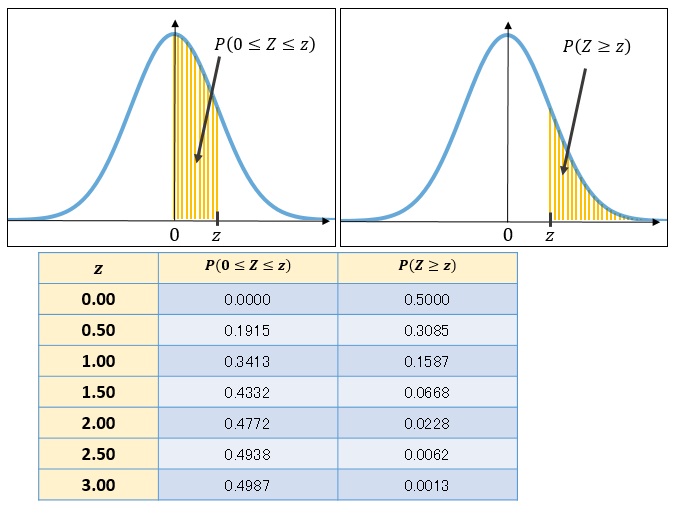



正規分布とは何なのか その基本的な性質と理解するコツ アタリマエ




Rで多次元正規分布に従う乱数を生成する 年金運用の例題付き




分かりやすい統計学 標準正規分布による確率計算と分布表の見方 ミナピピンの研究室




正規分布を標準化する方法と意味と例題と証明 Avilen Ai Trend




チョコっと正規分布



19 2 母平均の信頼区間の求め方 母分散既知 統計学の時間 統計web




小学生でも分かる正規分布




t分布と正規分布の違いは 母平均の推定 検定でどのように使い分けるかを解説 科学センスを目指して
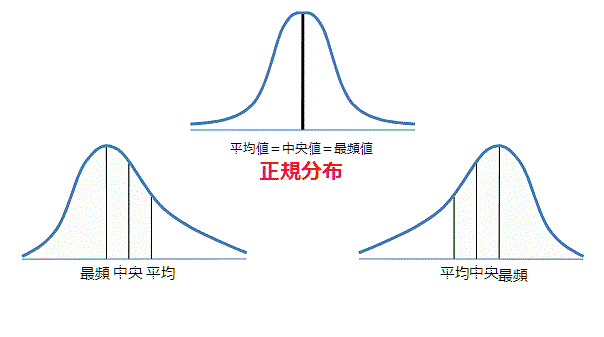



正規分布の分かりやすいまとめ Avilen Ai Trend



14 1 正規分布 統計学の時間 統計web




二次元正規分布の導出 Nishiru3の日記



0 件のコメント:
コメントを投稿